Since the frequency response of the realizable filter should be a continuous function, the magnitude response of a lowpass filter is specified with some acceptable tolerance. Moreover, a transition band is specified between the passband and stop band to permit the magnitude to drop off smoothly. Figure (9.2) illustrates this

Fig 9.2

In the passband magnitude the frequency response is within of unity

In the stopband

The frequencies and are respectively, called the passband edge frequency and the stopband edge frequency. The limits on tolerances and are called the peak ripple value. Often the specifications of digital filter are given in terms of the loss function , in dB. The loss specification of digital filter are

Some times the maximum value in the passband is assumed to be unity and the maximum passband deviation, denoted as is given the minimum value of the magnitude in passband. The maximum stopband magnitude is denoted by. The quantity   is given by

Fig 9.3

If the phase response is not specified, one prefers to use IIR digital filter. In case of an IIR filter design, the most common practice is to convert the digital filter specifications to analog low pass prototype filter specifications, to determine the analog low pass transfer function 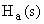meeting these specifications, and then to transform it into desired digital filter transfer function. This methods is used for the following reasons:

1. Analog filter approximation techniques are highly advanced.

2. They usually yield closed form solutions.

3. Extensive tables are available for analog-design.

4. Many applications require the digital solutions of analog filters.

The transformations generally have two properties (1) the imaginary axis of the s-plane maps into unit circle of the z-plane and (2) a stable continuous time filter is transformed to a stable discrete time filter.