where 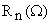 is
Chebyshev rational function of O determined from
specified ripple characteristics. is
Chebyshev rational function of O determined from
specified ripple characteristics.
An nth order Chebyshev filter
has sharper cutoff than a Butterworth filter,
that is, has a narrower transition bandwidth.
Elliptic filter provides the smallest transition
width. |