In the previous section, digital filters were designed to give a desired frequency response magnitude without regard to the phase response. In many cases a linear phase characteristics is required through the passband of the filter. It can be shown that causal IIR filter cannot produce a linear phase characteristics and only special forms of causal FIR filters can give linear phase.

If represents the impulse response of a discrete time linear system a necessary and sufficient condition for linear phase is that have finite duration N , that it be symmetric about its mid point, i.e.

For N even, we get

For N odd

For N even we get a non-integer delay, which will cause the value of the sequenceto change, [See continuous time implementation of discrete time system, for interpretation of non-integer delay].

One approach to design FIR filters with linear phase is to use windowing.

The easiest way to obtain an FIR filter is to simply truncate the impulse response of an IIR filter. If 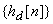is the impulse response of the designed FIR filter, then an FIR filter with impulseresponse 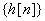can be obtained as follows.

This can be thought of as being formed by a product of and a window function

where is said to be rectangular window and is given by

Using modulation property of Fourier transfer

For example if is ideal low pass filter and is rectangular window is measured version of the ideal low pass frequency response.

Fig  9.5

In general, the index the main lobe of , the more spreading where as the narrower the main lobe (larger N), the closer comes to. In general, we are left with a trade-off of making N large-enough so that smearing is minimized, yet small enough to allow reasonable implementation. Much work has been done on adjusting to satisfy certain main lobe and side lobe requirements. Some of the commonly used windows are give in below.  

(a) Rectangular

(b) Bartlett (or triangle)

(c) Hanning

(d) Harming

(e) Blackman

(f) Kaiser

where is modified zero-order Bessel function of the first kind given by

The main lobe width and first side lobe attenuation increase as we proceed down the window listed above.

An ideal lowpass filter with linear phase and cut off is characterized by

The corresponding impulse response is

Since this is symmetric about , if we change and use one of the windows listed above the will get linear phase FIR filter. Transition width and minimum stopped attenuation are listed in the Table 9.3.

We first choose a window that satisfies the minimum attenuation. The transition bandwidth is approximately that allows us to choose the value of N. Actual frequency response characteristic are then calculated and we see if the requirements are met or not. Accordingly N is adjusted parameters for kaiser window are obtained from design formula available for this MATLAB or similar programmes have all there formulas.