Signals in Natural Domain
Chapter 7 :  The Z-transform
 
System Function and block diagram representation

The use of z-transform allows us to replace time domain operation such as convolution time shifting etc with algebraic operations.
Consider the parallel interconnection if two system, as shown in figure 7.4.



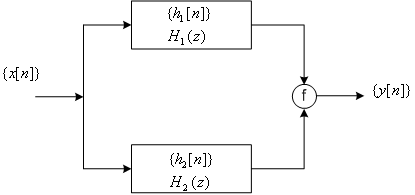
Fig  7.4


The impulse response of the over all system is

$\displaystyle \{h[n]\}=\{h_{1}[n]\}+\{h_{2}[n]\}$

From linearity of the z-transform,
$\displaystyle H(z)=H_{1}(z)+H_{2}(z)$

Similarly, the impulse response of the series connection in figure 7.5 is
$\displaystyle \{h[n]\}=\{h_{1}[n]\}*\{h_{2}[n]\}$


Fig 7.5



From the convolution property.

$\displaystyle H(z)=H_{1}(z)H_{2}(z)$

The z-transform of the interconnection of linear system can be obtained by algebraic means. For example consider the feed back connection in figure 7.6



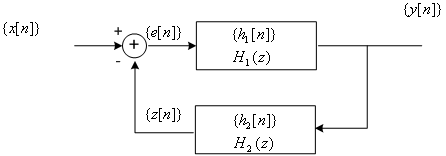
Fig 7.6


We have

$\displaystyle Y(z)$ = $\displaystyle H_{1}(z)E(z)$  
$\displaystyle E(z)$ = $\displaystyle X(z)-Z(z)$  
  = $\displaystyle X(z)-Y(z)H_{2}(z)$  
or$\displaystyle \qquad\qquad \,\,Y(z)$ = $\displaystyle H_{1}(z)[X(z)-Y(z)H_{2}(z)]$  
$\displaystyle \frac{Y(z)}{X(z)}$ = $\displaystyle H(z)=\frac{H_{1}(z)}{1+H_{1}(z)H_{2}(z)}$  
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
1