![$\displaystyle \{x[n]\}*\{y[n]\}\leftrightarrow X(z)Y(z),\,\,$](images/img111.png) ROC contains 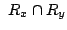
The z-transform of the convolution is
![$\displaystyle \sum\limits^{\infty}_{n=-\infty}(\sum\limits^{\infty}_{k=-\infty}x[k]y[n-k])z^{-n}$](images/img113.png)
Interchanging the order of summation
![$\displaystyle =\sum\limits^{\infty}_{k=-\infty}x[k]\sum\limits^{\infty}_{n=-\infty}y[n-k]z^{-n}$](images/img114.png) using time shifting property (or changing index of summation)
using time shifting property (or changing index of summation)
| |
= |
![$\displaystyle \sum\limits^{\infty}_{k=-\infty} x[k]z^{-k}Y(z)$](images/img115.png) |
|
| |
= |
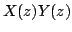 |
|
If there is pole-zero cancelation, the ROC will be larger than the common ROC of two sequence.
Convolution property plays an important role in analysis of LTI system. An LTI system, which produces a delay of 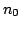 , has the transfer function , has the transfer function
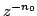 , therefore delay of , therefore delay of 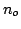 units is often depicted by units is often depicted by
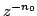
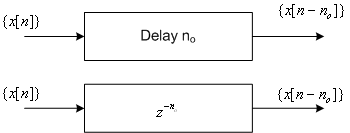
Fig 7.3
|