This is method is useful when z-transform is ratio of polynomials. A rational 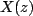 can be expressed as can be expressed as
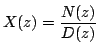
where 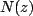 and and 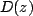 are polynomials in. If degree are polynomials in. If degree 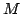 of the numerator polynomial of the numerator polynomial 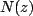 is greater than or equal to the degree N of the denominator polynomial is greater than or equal to the degree N of the denominator polynomial 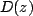 , we can divide , we can divide 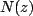 by by 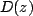 and re-express and re-express 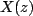 as as
![$\displaystyle X(z)=\sum\limits^{M-N}_{k=0}a[k]z^{-k}+\frac{N_{1}(z)}{D(z)}$](images/img130.png)
where the degree of polynomial 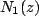 is strictly less than that of. For simplicity let us assume that all poles are simple. Then is strictly less than that of. For simplicity let us assume that all poles are simple. Then 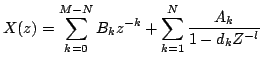
where
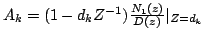
Example: Let
The partial fraction expression is
The inverse z-transform depends on the ROC. If ROC is
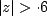 , then ROCs associated with each term is outside a circle(so that common ROC is outside a circle), sequences are causal. Using linearity property and z-transform of , then ROCs associated with each term is outside a circle(so that common ROC is outside a circle), sequences are causal. Using linearity property and z-transform of ![$ a^{n}u[n]$](images/img142.png) we get we get
![$\displaystyle x[n]=2.75(0.2)^{n} u[n]-1.75(-.6)^{n}u[n]$](images/img143.png)
If the ROC is
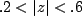 , the ROC of the term , the ROC of the term
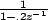 should be outside the circle should be outside the circle 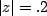 , and ROC for , and ROC for
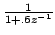 should be. Hence we get the sequence as should be. Hence we get the sequence as
Similarly if ROC is 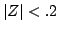 we get a noncausal sequence we get a noncausal sequence
If 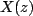 has multiple poles, the partial fraction has slightly different form. If has multiple poles, the partial fraction has slightly different form. If 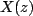 has a pole of order s at has a pole of order s at 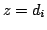 , and all other poles are simple Then , and all other poles are simple Then
where 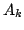 and and 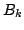 are obtained as before, the coefficients are obtained as before, the coefficients 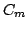 are given by are given by
If there are more multiple poles, there will be more terms like the third term.
Using linearity and differentiation properties we get some useful z-transform pairs given in Table 7.2
|