| |
| Properties of the ROC |
- The ROC of
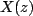 consists of an annular region in the z-plane, centered about the origin. This property follows from equation (7.3), where we see that convergence depends on consists of an annular region in the z-plane, centered about the origin. This property follows from equation (7.3), where we see that convergence depends on 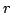 only. only.
- The ROC does not certain any poles. Since at poles
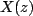 does not converge. does not converge.
- The ROC is a connected region in z-plane. This property is proved in complex analysis.
- If
![$ \{x[n]\}$](images/img17.png) is a right sided sequence, i.e. is a right sided sequence, i.e. ![$ x[n]=0$](images/img52.png) , for , for 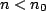 , and if the circle , and if the circle
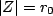 is in the ROC, then all finite values of is in the ROC, then all finite values of 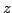 , for which , for which
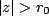 will also be in the ROC. will also be in the ROC.
For a right sided sequence
If 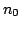 is negative then we can write is negative then we can write
![$\displaystyle X(z)=\sum\limits^{0}_{n=n_0}x[n]z^{-n}+\sum\limits^{\infty}_{n=1}x[n]z^{-n}$](images/img58.png) Let
Let 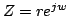 , with , with 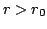 , then, , then, 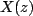 exists if exists if
![$ \sum\limits^{-1}_{n=n_{0}}\vert x[n]\vert
r^{-n}+\sum\limits^{\infty}_{n=0}\vert x[n]\vert r^{-n}$](images/img61.png) is finite. is finite.
The first summation is finite as it consists of a finite number of terms. In the second summation note that each term is less than
![$ \vert x[n]\vert r^{-n}_{0}$](images/img62.png) as. Since as. Since
![$ \sum\limits^{\infty}_{n=1}
\vert x[n]\vert r^{-n}_{0}$](images/img63.png) is finite by our assumption that circle with radius is finite by our assumption that circle with radius 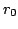 lies in ROC, the second sum is also finite. Hence values of z such that lies in ROC, the second sum is also finite. Hence values of z such that
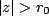 lies in ROC, except when. At lies in ROC, except when. At 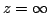 , the first summation will became infinite. So if , the first summation will became infinite. So if
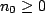 , i.e. the sequence , i.e. the sequence ![$ x[n]$](images/img67.png) is causal, the value is causal, the value 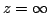 will lie in the ROC. will lie in the ROC.
- If
![$ \{x[n]\}$](images/img17.png) is left sided sequence, i.e. is left sided sequence, i.e.
![$ x[n]=0,\,n>n_0$](images/img68.png) and and
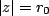 lies in the ROC, the values of lies in the ROC, the values of 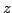 function function
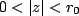 also lie in the ROC. also lie in the ROC.
The proof is similar to the property 4. The point 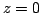 , will lie in the ROC if the sequence is purely , will lie in the ROC if the sequence is purely
anticausal
![$ (x[n]=0,\,n>0)$](images/img71.png)
- If
![$ \{x[n]\}$](images/img17.png) is non zero for, is non zero for,
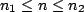 , then ROC is entire z-plane except possibly , then ROC is entire z-plane except possibly 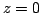 , and/or.
In this case the , and/or.
In this case the 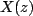 consists of finite number of terms and therefore it converges if each term infinite which is the case when consists of finite number of terms and therefore it converges if each term infinite which is the case when 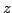 is different from 0 or. is different from 0 or. 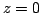 lies in ROC, if lies in ROC, if
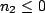 , and , and 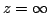 lies in the ROC if. lies in the ROC if.
- If
![$ \{x[n]\}$](images/img17.png) is two-sided sequence and if circle is two-sided sequence and if circle
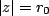 is in ROC, then ROC will consist of annular region in z-plane, which includes.
We can express a two sided sequence as sum of a right sided sequence and a left sided sequence. Then using property 4 and 5 we get this property. Using is in ROC, then ROC will consist of annular region in z-plane, which includes.
We can express a two sided sequence as sum of a right sided sequence and a left sided sequence. Then using property 4 and 5 we get this property. Using
property 2 and 3 we see what ROC will be banded by circles passing through the poles.
|
| |
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|