This shows that
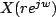 is Fourier transform of the sequence. When is Fourier transform of the sequence. When 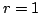 the z-transform reduces to the Fourier transform of. From equation (7.3) we see that for convergence of z-transform that Fourier transform of the sequence the z-transform reduces to the Fourier transform of. From equation (7.3) we see that for convergence of z-transform that Fourier transform of the sequence
![$ \{r^{-n}x[n]\}$](images/img26.png) converges. This will happen for some r and not for others. The values of z - for which converges. This will happen for some r and not for others. The values of z - for which
![$ \sum\limits^{\infty}_{n=-\infty} r^{-n} \vert x[n]\vert < \infty$](images/img28.png) is called the region of convergence(ROC). If the ROC contains unit circle (i.e. is called the region of convergence(ROC). If the ROC contains unit circle (i.e. 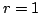 or equivalently or equivalently 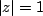 then the Fourier transform also converges. Following examples show that we must specify ROC to completely specify the z-transform. then the Fourier transform also converges. Following examples show that we must specify ROC to completely specify the z-transform.
|