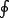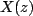the symbol indicates contour integration, over a counter clockwise contour in the ROC of. If consists of ratio of polynomials one can use Cauchy integral theorem to calculate the contour integral. There are some other alternative procedures also, which will be considered after discussing the properties of z-transform.
![$\displaystyle x[n]=\frac{1}{2 \pi j}\oint X(z)z^{n-1}dz$](images/img76.png)
indicates contour integration, over a counter clockwise contour in the ROC of. If 
consists of ratio of polynomials one can use Cauchy integral theorem to calculate the contour integral. There are some other alternative procedures also, which will be considered after discussing the properties of z-transform.
