Concluding remarks
To summarise, the present chapter considered rotor dynamics aspect of rolling bearings, hydrodynamic bearings, seals, and squeeze-film dampers. The main aim is to obtain the stiffness, damping, and inertia effects of these supports on to the rotor. For rolling element bearings a comparative study is provided of several of kinds of bearings and then load-deflection relations are obtained for simple to more general cases. The procedure of calculation of the linear and nonlinear stiffness is described in detailed. For fluid film hydrodynamic bearings the basic Reynolds equation is described and the procedure of calculation of the linearised stiffness and damping coefficients for short and finite bearings are provided. These dynamic parameters are found to be rotor speed dependent.  Various kinds of rotary seals are described with their application area. The governing equation of seal dynamics based on bulk fluid theory is described and for simple case the damping and stiffness coefficients are obtained and discussed in detailed. Squeeze-film dampers are introduced and their rotordynamic parameters are summarised. These dynamic parameters of bearings, seals and dampers have been obtained at present in isolation of the shaft dynamics. However, in subsequent chapters we will integrate the dynamics of the rotor and bearing together so that the free and forced response behaviour of the rotor can be predicted accurately. This includes the calculation of whirl natural frequencies, critical speeds, and instability of the rotor-bearing system.

Exercise Problems

Exercise 3.1 List down parameters on which the stiffness of rolling element bearings depends.

Exercise 3.2 List down parameters on which the stiffness and damping coefficients of fluid film hydrodynamic bearings and seals depend.

Exercise 3.3 The specification of the ball and roller bearings are given in Table E3.2. Plot the variation of the bearing radial stiffness versus the elastic radial deformation. Show the variation for different radial clearances. Take increments in the load of 100 N and that of the radial clearance as 0.005 mm for plotting the variation of the radial stiffness.

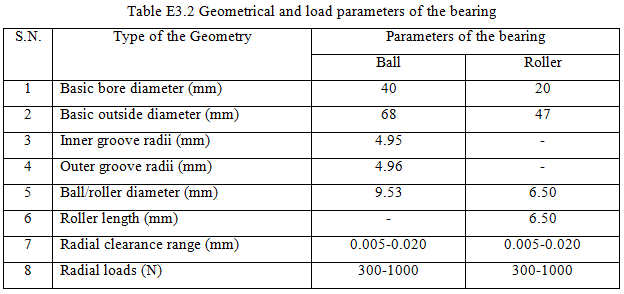
Exercise 3.4 For exercise problem 3.3, obtain the variation of stiffness of the ball and roller bearings for different orientation of the rolling elements (i.e., for different values of Φ). Discuss the results obtained.

Exercise 3.5 Obtain the plots of non-dimensional the stiffness and damping coefficients versus the Sommerfeld number (between 0.01 to 10) for the short bearing assumption of a hydrodynamic bearing.

Exercise 3.6 Choose a single answer from multiple choice answers

1. A high-speed hydrodynamic bearing is modelled by linearised coefficients, these coefficients are
1. stiffness & damping
2. virtual or added mass
3. both (A) & (B)
4. None of the above
2. The hydrodynamic fluid-film bearing is governed by
1. Bernoulli equation
2. Reynolds equation
3. Navier-Strokes equation
4. Maxwell equation
3. For variable speed and load conditions, the most appropriate bearing would be
1. Squeeze-film bearing
2. Fluid-film bearing
3. Gas bearing
4. Rolling element bearing
4. For the attenuation of rotor vibrations at the resonance, the machine element used is
1. Seal
2. Fluid-film bearing
3. Rolling element bearing
4. Squeeze-film bearing
5. For a short-bearing approximation in the fluid-film bearing analysis
1. (K) The radial and circumferential pressure gradients are negligible
2. (λ) The radial and axial pressure gradients are negligible
3. (μ) The radial pressure gradient is negligible
4. (v) The circumferential and axial pressure gradients are negligible