where x and y are displacements in the x- and y-axes directions, respectively; single and double dots represent one and two times derivative with respect to time, respectively; c and m are damping and inertia coefficients, respectively, of the damper fluid-film with their subscripts denote force and motion directions respectively; and f is the fluid-film force and its subscript denote the direction of application. For short length open ends squeeze-film damper, the rotordynamic coefficients are given as (for no cavitations i.e. the full film model)

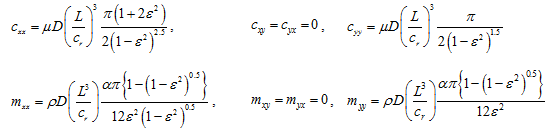
with

(3.130)

where ranges from 1.2 to 1.0 for small to moderately large squeeze-film Reynolds numbers (); L, D, and c_r represent the damper axial length, diameter, and radial clearance, respectively; ρ and µ are the fluid density and viscosity, respectively; and e is the eccentricity ratio. Expressions are valid for the isoviscous and incompressible fluids undergoing isothermal process within the damper. For short length open ends squeeze-film damper, the rotordynamic coefficients are given as (with cavitations, i.e. the half-film model)

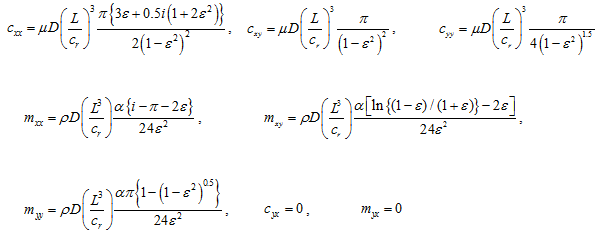
with

(3.131)

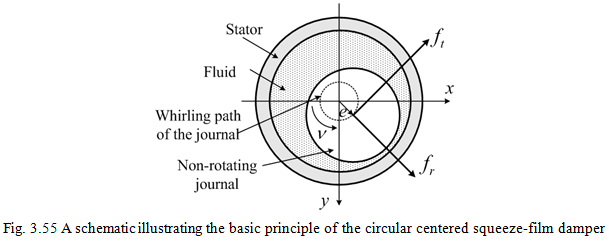
For circular centered journal (i.e., the outer ring in rolling bearings or the bush in fluid-film bearings) motions (Fig. 3.55) of the amplitude, e, and whirl frequency, ν, in a perfectly cylindrical bearing, a damper produces a constant fluid force in a reference frame rotating with angular frequency of, ν. The radial and tangential components of the fluid force are equal to

(3.132)

with

(3.133)

where V_t and a_r are the tangential velocity and the radial acceleration, respectively, of the journal centre; (c_rt, c_tt) and (m_rr, m_tr) are the cross-coupled and direct damping and inertia force coefficients, respectively. It should be noted that these linearised coefficients are defined for small motions only. For the short-length approximation, -film assumption (i.e., half the circumferential film extend is cavitated) and open ends squeeze-film damper model, the force coefficients are given as (Vance, 1988)

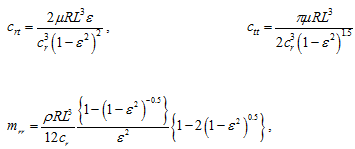
and

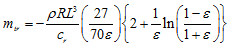(3.134)

where L, D, and c_r represent the damper axial length, diameter, and radial clearance, respectively; ρ and μ are the fluid density and viscosity, respectively; and ε is the eccentricity ratio. Expressions are valid for the isoviscous and incompressible fluids undergoing isothermal process within the damper. For the short-length approximation, 2-film assumption (i.e., no cavitations) and open ends squeeze-film damper model, the force coefficients are given as

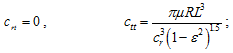
and

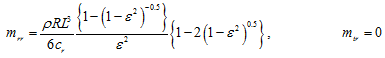(3.135)

It should be noted that cross-coupled coefficients are zero and direct coefficients are doubled as compared to the -film assumption. A large clearance, low viscosity and high whirl frequency would lead to appreciable inertia coefficients and may change drastically the rotor-damper dynamic response. Tichy and Modest (1978), and San Andres and Vance (1987) provided fluid inertia coefficients for finite length dampers. Tao et al. (2000) presented analysis of squeeze film dampers operating in bubbly lubricants. A continuum model was proposed for describing the motion of a bubbly fluid in an open ended SFD operating with circular centered journal orbits. Computed predictions for peak-peak dynamic pressures and fluid film forces were compared with experimental measurements conducted on a SFD test rig operating with a controlled air in oil mixture.  Pietra and Adietta (2002), and Adietta, and Pietra (2002) gave a comprehensive survey of the squeeze film damper investigations in two parts. In the first part, a survey of the construction characteristics and operating features of the SFD, as a separate component, was reported, as inferred from the technical literature consulted, through a number of theoretical approaches and experimental results. The second part of the paper reviewed research work on the dynamic behavior of rotors on supports equipped with SFDs. Because of the complexity in the analysis of squeeze-film dampers, often practice engineers prefer to find the rotordynamic properties through experiments (Tiwari et al., 2004 and 2005).