Finite Fourier Transform

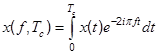
Power Spectrum / Autospectrum / Autospectral density function or Power spectral density function can be obtained by using the following equation.

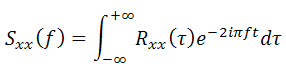
where

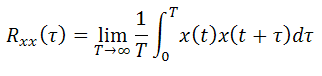
Also it can be obtained using the following equation.

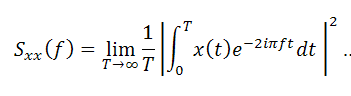
Exercise Problem

1.Write a Matlab code using Newton Raphsons method to solve the following characteristics equations. Check the results using method of bisections.

(a)

(b)

2. Compute the integrals given in equation (5.1.10). You may use the int function of the Matlab. Use dummy variables while performing double and triple integration. Also write a Matlab code using 12 point Gauss-Quadrature and compare the results. Find the coefficients of the temporal equation of motion.

3.Solve the frequency response equation obtained from the Duffing equation which is quadratic in terms of the detuning parameter and 6 ^th order in terms of amplitude of the response.

4. Use Runge-Kutte method (may use ode45 function of Matlab) to obtain the time response of the following equations.

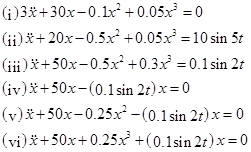
Reference :

1. B. Pratiher and S. K. Dwivedy, Nonlinear dynamics of flexible single –link Cartesian Manipulator, International Journal of Nonlinear Mechanics Vol. 42 , pp1062-1073, 2007.

2. B. Pratiher and S. K. Dwivedy, Nonlinear Vibration of a Single Link Viscoelastic Cartesian Manipulator, International Journal of Nonlinear Mechanics Vol. 43 , pp 683-696, 2008 .

3.   A. H. Nayfeh, and B. Balachandran, Applied Nonlinear Dynamics , Wiley, 1995.

4. J. D. Hoffman Numerical Methods for Engineers and Scientists, CRC Press, London, 2001

5. T.W. Cooley and J. W. Tukey, 1965 An algorithm for the machine calculation of complex Fourier series, Math. Comp,19,297-301