Finite Difference Method

• •  Forward Difference Method
  
• •  Backward difference Method
• 
  •  Central difference method ( Most accurate )
• 
  Central difference method ( Most accurate)
• 
  
  •  Replace the solution domain with finite number of points (mesh or grid point)
  
• •  Using Taylor's series expansion

• Replace the solution domain with finite number of points (mesh or grid point)

• Using Taylor's series expansion

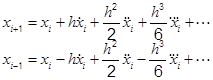
RUNGE-KUTTA METHOD

Here the approximate formula used for obtaining from is made to coincide with the Taylor series expansion of x at up to terms of order . The Taylor series of expansion of
x ( t ) at t + Δ t is given by-

Example:

• For a viscously damped single degree of freedom nonlinear system, we can write

The value of at any time t can be given by using 4^th order Runge-Kutte method using the following formula.
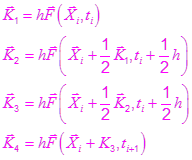