NEWMARK METHOD

• • This method is also based on the assumption that the acceleration varies linearly between two instant of time.
• 
  • The resulting expression for the velocity and displacement respectively can be written for multi degree of freedom as,

• here α and β indicates how much the acceleration at the end of the interval enters into the velocity and displacement equations at the end of the interval Δt .
• 
  • The equilibrium equation of motion of a viscously damped multi degree of freedom system at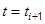 can be written as:
  
• 
• 
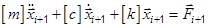
  • Using above equations we can obtain a relation to find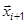

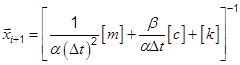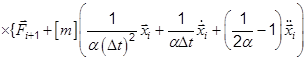• After obtaining the time response one may be interested to know the frequency content of the time response by performing the Fourier transform using the following equation.
• 
• 
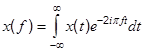
  Assumption that the function is integrable can be checked by using the following
•