In this lecture, the basic numerical tools used in the study of nonlinear dynamics of a system will be briefly reviewed. It may be recalled from the derivation of equation of motion in module 2 that it is not always possible to use simple expressions or closed form analytical solutions and hence, one requires numerical operations to solve the problems. Generally following numerical tools are required.

• •  Numerical differentiation
  •  Numerical integration
  •  Finding roots of the algebraic or transcendental equation
  •  Solving differential equation
  •  Finding eigenvalues
  •  Poincare' section
  •  Lyapunov exponent

For example consider the system whose equation of motion we have derived in module 2.

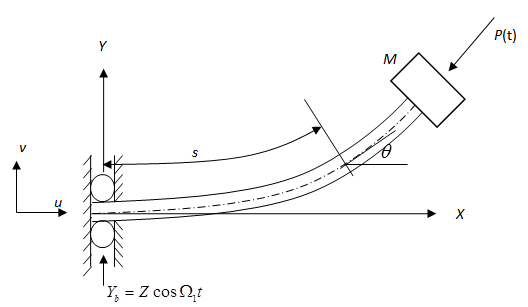
Figure 5.1.1: Schematic diagram of a single-link Cartesian manipulator with payload subjected to harmonically varying axial force.

Figure 5.1.1 shows the system with a payload of mass m at the tip where a compressive force
P = is applied. Also this system is subjected to a harmonic base excitation
= at the roller supported left end. Here Z and are the amplitude and frequency of the base excitation, , are the static and dynamic force amplitude, and is the frequency of the periodic force acting at the free end of the manipulator. The motion is considered to be in the vertical plane.