Here, 
and 
are the Young modulus, moment of inertia, mass density, area of cross-section, length of the cantilever beam and damping factor of the system and 
respectively, are used as integration variables. The following non-dimensional parameters are used in the further analysis.
, 
, 
, 
, 
, 
, 
, 
, and 
.
Also, the eigenfunction for a cantilever beam with a tip mass is given by
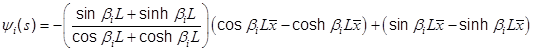(5.1.11)
One may determine 
from the following equation.
.............................. (5.1.12)
One may note that the coefficients of the temporal equation can be obtained by first finding the roots of the characteristic equation (5.1.12) and there by finding the integration 
to 
which also requires numerical differentiation. Following numerical methods may be used for finding the roots of the characteristic equation.
- o Interval halving-Method of Bisection
o False position (Regula Falsi)
- o Newton's method
o Secant Method
- o Muller's method
Let us consider a function 
. According to method of bisection one should choose two values of x for example 
and 
such that, one of the functional value should be positive and other should be negative. Now the next point is obtain by interval halving, i.e., 
. The root is now assumed to lie between and 
if their functional values are of opposite sign. Otherwise, it will lie between and . The next point is obtained by halving the interval and the procedure is repeated till obtain a root having the functional value within a very close tolerance.
In Newton's method which is also known as Newton-Raphson's method one finds the derivative to obtain the root. As shown in Fig. (5.1.2), the actual solution is 
. Choosing 
as the guess value of the root