Taking ,

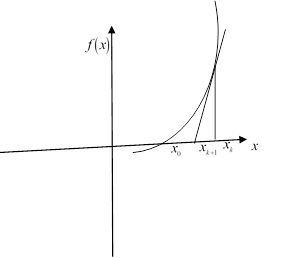
Figure 5.1.2: Illustration of Newton-Raphson method

It may be noted that point is closer to the actual solution . Now taking as the guess value the iteration is repeated till the functional value is within the tolerance limit.

In secant method

In Muller method

For a system of equations, one may use Newton's method.

To solve the differential equations following methods may be used

• • The finite difference method,
• 
  • The Runge-Kutta method,
  
• • The Wilson method,
• 
  • The Newmark method.