Review of Linear system

Single Degree of Freedom Systems

Steady state response due to Harmonic Oscillation

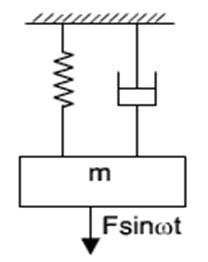
Fig 1.1.7 Spring -mass-damper system subjected to harmonic excitation

Equation of motion of the system with mass m, stiffness k, damping factor c and forcing amplitude F and forcing frequency ω can be given by the following equation.

..............................................................................................(1.1.14)

This can also be written as

...............................................................................(1.1.15)

Here, is the natural frequency, is the damping ratio of the system.

For free vibration of the system the forcing term can be made zero and the equation can be written as

........................................................................................................... (1.1.16)

Free Vibration response of the system

• For undamped system ( )

........................................................................................... (1.1.17)

Here a and b are constants to be determined from the initial conditions. The system will vibrate with natural frequency and the response amplitude depends on the initial displacement and velocity of the system.

• For under damped system

.........................................................................(1.118)

where X and ψ are constants to be determined from initial coditions.

• For critically damped system

• For over damped system