Generalized coordinate : These are a set of independent coordinates same in number as that of the vibrating system. For example, the motion of a double pendulum in planar motion can be represented completely either by 
the rotation of the first and second link respectively or by 
the Cartesian coordinates of first and second links. While in the later case 4 coordinates are required to represent completely the system, in the former case only 2 coordinates are required for the same. Hence, in this case is the generalized co-ordinate while are not the generalized one. One may note that these four coordinates are not independent and can be reduced to two by the use of length constraint.
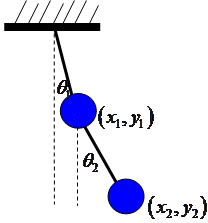
Fig. 1.1.4. Illustration of physical and generalized coordinates in a double pendulum
Newton's second law A partical acted upon by a force moves so that the force vector is equal to the time rate of change of the linear momentum vector.
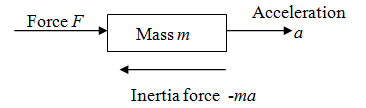
Fig. 1.1.5 Application of Newton's second law
Taking, 
-initial velocity, 
-final velocity, and t time, according to Newton's 2 nd law
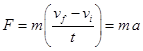.........................................................................................(1.1.5)
Work energy principle
The work performed by a force in moving a particle of Mass M from position 
to 
is equal to the change in kinetic energy.
...................................................(1.1.6)
Here T1 and T2 are the Kinetic energy in position 1 and 2 respectively.
It can be shown that
- • Force for which the work performed in moving a particle over a closed path is zero (considering all possible paths) is said to be conservative force .