In case , the operator D and hence the system is said to posses homogeneity property and when the system is said to posses additive property. If an operator D does not possess the homogeneity and additivity property the system is said to be nonlinear.

Example 1: Check whether system given by the following is linear or nonlinear

..............................................(1.1.1)

where, ε is a const ant

Solution: check the homogeneity

≠ αD(t) .............(1.1.2)

Hence homogeneity condition is not satisfied

Similarly substituting ......................................................................... (1.1.3)

One obtains

.................................................................................. (1.1.4)

which does not satisfy additive property also. Hence the system is a nonlinear system. It may be noted that, the term containing ε causes the nonlinearity of the system. If the equation becomes linear by satisfying both homogeneity and additive properties.

Hence it may be observed that

• 1) A system is linear if the function 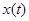and its derivatives appear to the first (or zero) power only; otherwise the system is nonlinear.
• 
  2) A system is linear if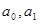 and 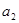depend as time alone, or they are constant.

Steps for Vibration Analysis

• • Convert the physical system to simplified mathematical model
  •
• Determine the equation of motion of the system
• 
  • Solve the equation of motion to obtain the response
• 
  • Interpretation of the result for the physical system.

To convert the physical system into simpler models one may use the concept of equivalent system. To determine the equation of motion basically one may use either the vector approach with the Newtonian approach or d'Alembert principle based on free body diagram or one may go for scalar approach using the energy concept. In scalar approach one may use Lagrange method, which is a differential procedure or extended Hamilton's principle based on integral procedure. Different methods/laws/principle used to determine the equations of motion of the vibrating systems are briefly introduced below. In module 2 they are described in detail.

Derivation of Equation of motion

  Depending on coordinate:

In Newtonian mechanics motions are measured relative to an inertial reference frame, i.e, a reference frame at rest or moving uniformly relatively to an average position of “ fixed stars” and displacement, velocity and acceleration are absolute values.