Nonlinear Vibration : If one or more basic components of a vibratory system are not linear then the system is nonlinear. All most all the system can be modelled as a nonlinear system.

Depending on excitation:

Deterministic : If the value or magnitude of the excitation (force or motion) acting on a vibratory system is known at any given time, the excitation is called deterministic. The resulting vibration is known as deterministic vibration.

Random Vibration: In this case the value of the excitation at any given time can not be predicted. Example Wind velocity, road roughness and ground motion during earth quake etc.

 

2. Linear and Nonlinear systems

A system is said to be linear or nonlinear depending on the force response characteristic of the system. The block diagram relating to output and input can be represented as shown in Fig 1.1.2(a) and mathematically represented as shown in Fig. 1.1.2(b).

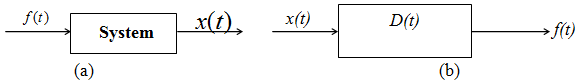
Fig.1.1. 2: (a) Block diagram showing the force-response and (b) mathematical representation of the input and the output through the operator D(t) .

A linear system may be of first or second order depending on the presence of the basic elements. A typical first order system with linear spring and viscous damping is shown in Fig. 1.1. 3(a) and that of a second order system is shown in Fig.1.1.3 (b) as they can be represented by and respectively.

As shown in Fig. 1.1 2(b), a system can be represented by using a operator D such that Dx(t) = f(t) , where D is the differential operator, x ( t ) is the response and f ( t ) is the excitation input.

A system is said to be linear if it satisfies the following two conditions.

1. 1. The response to 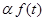is 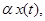where α is a constant.
   2.
2. The response to 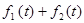is 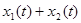where the 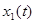is the response to 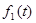and 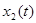is the response to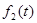

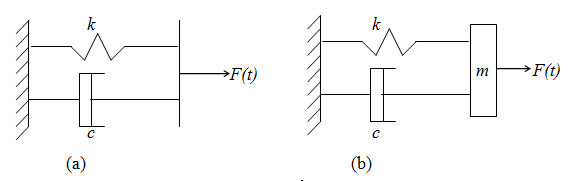
Fig 1.1.3(a) First order system (b) second order system