where k = 1, 2,… n, n = no of dof of the system. The extended Hamilton's principle is very general and can be used for a large variety of systems. The only limitation is that the virtual displacement must be reversible which implies that the constraint forces must perform no work. Principle cannot be used for system with friction forces.
In general 
(subscript c refers to conservative and nc refers to the nonconservative). Also, 
. Now introducing Lagrangian 
, the extended Hamilton's principle can be written as
, 
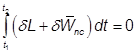,........................................................ (1.1.10)
where k = 1,2,….. n
For conservative system 
, Eq. (1.1.10) reduces to
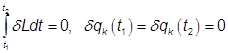............................................................................ (1.1.11)
which is known as the Hamilton's Principle.
Lagrange Principle
The Lagrange principle for a damped system can be written as
.....................................................................................(1.1.12)
where
..................................................................(1.1.13)
where L is the Lagrangian given by L=T-U , T is the kinetic energy and U is the potential energy of the system. D is the dissipation energy and Qk is the generalized force. Fi and Mi are the vector representation of the externally applied forces and moments respectively, the index k indicates which external force or moment is being considered, ri is the position vector to the location where the force is applied, and 
is the system angular velocity about the axis along which the considered moment is applied.
Modeling of the system
- • Single degree of freedom system
• Two degree of freedom system
- • Multi-degree of freedom system
• Continuous system