- • Work performed by a conservative force in moving a particle from
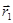to 
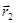is equal to the negative of the change in potential energy from V1 to V2
• Work performed by the nonconservative forces in carrying a particle from position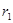
to position 
is equal to the change in total energy
d'Alembert Principle The vectorial sum of the external forces and the inertia forces acting on a moving system is zero. Referring to Fig.1.1.5. according to d'Alembert Principle 
where 
is the inertia force.
Generalized Principle of d'Alembert:
The virtual work performed by the effective forces through infinitesimal virtual displacements compatible with the system constraints is zero.
................................................................................................. (1.1.7)
Extended Hamilton's Principle
For a system with Number of particles we can conceive of a 3N dimensional space with the axes 
, 
, 
and represent the position of the system of particles in that space and at any time t the position of a representative point P with coordinate 
, 
, 
where i = 1,2,… N. The 3N dimensional space is known as the Configuration Space. As time unfolds, the representative point P traces a curve in the configuration space called the true path, or the Newtonian path, or the dynamical path. At the same time let us think of a different representative point 
resulting from imagining the system in a slightly different position defined by the virtual displacement 
(i = 1,2… N ). As time changes the point traces a curve in the configuration space known as the Varied Path.
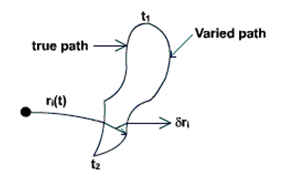
Fig1.1.6: True and Varied path
Of all the possible varied path, now consider only those that coincide with the true path at the two instants 
and 
as shown in Fig.1.1.6. The Extended Hamilton's Equation in terms of Physical coordinates can be given by
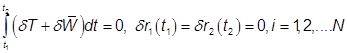................................................(1.1.8)
where 
is the variation in kinetic energy and 
is the variation in the work done. But in many cases it is desirable to work with generalized coordinates q. As and are independent of coordinates so one can write
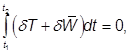
....................................................................(1.1.9)