- Describe a path in
 whose image under the standard map represents the generator of
whose image under the standard map represents the generator of
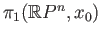 .
.
- Let
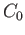 be the unit circle in the complex plane and
be the unit circle in the complex plane and
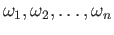 denote the
denote the 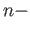 th
roots of unity and at each of these a circle
th
roots of unity and at each of these a circle 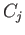 of small radius touches the unit circle externally. Construct a
continuous map
of small radius touches the unit circle externally. Construct a
continuous map  from the union of these
from the union of these 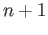 circles onto the figure eight loop such that
circles onto the figure eight loop such that  is a regular covering.
Hint: Take one lobe of the figure eight to be the unit circle
is a regular covering.
Hint: Take one lobe of the figure eight to be the unit circle 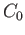 and define
and define
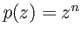 for
for 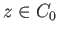 .
Let
.
Let 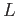 be the other lobe of figure eight touching the lobe
be the other lobe of figure eight touching the lobe 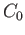 at say the point
at say the point 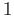 .
For each
.
For each 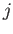 let
let
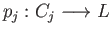 be any
homeomorphism such that
be any
homeomorphism such that
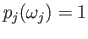 . Use gluing lemma to glue these maps to obtain the desired covering.
in
. Use gluing lemma to glue these maps to obtain the desired covering.
in
- For the covering projection of the preceding exercise determine the action of the fundamental group of the base on a fiber assuming that
the loops
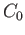 and
and 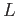 (based at
(based at 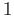 ) generate the fundamental group.
) generate the fundamental group.
- Consider the covering projection of exercise 6, lecture 15.
Show by studying the lifts of various loops based at
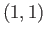 that the covering is regular.
We shall see another proof of regularity of this covering
in lecture 19.
that the covering is regular.
We shall see another proof of regularity of this covering
in lecture 19.
- For the covering considered in the preceding exercise, determine the lifts of the loops
Find the lift of
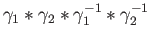 and deduce that the fundamental
group of the figure eight space is non-abelian.
and deduce that the fundamental
group of the figure eight space is non-abelian.
- Show that the figure eight loop
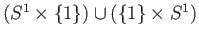 is not a retract of the torus
is not a retract of the torus
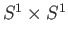 . Show that the figure eight
loop is a deformation retract of the torus minus a point.
. Show that the figure eight
loop is a deformation retract of the torus minus a point.
in
Lecture XVIII - The lifting criterion
We have already discussed the lifting problem and examined its significance in the light of complex analysis.
We have seen in connection with the
exponential map/squaring map that the existence of a lift of the inclusion map of a domain 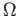 into
into
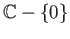 is equivalent to the existence of a continuous branch of the logarithm/square-root function on
is equivalent to the existence of a continuous branch of the logarithm/square-root function on 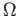 .
Thus it is desirable to
have a necessary and sufficient condition for the existence of lifts. We prove one such theorem in this
lecture which provides an
elegant necessary and sufficient condition.
.
Thus it is desirable to
have a necessary and sufficient condition for the existence of lifts. We prove one such theorem in this
lecture which provides an
elegant necessary and sufficient condition.
Subsections
nisha
2012-03-20