Since
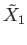 is simply connected the map
is simply connected the map 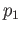 has a lift
has a lift
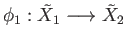 with respect to the covering projection
with respect to the covering projection
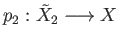 , such that
, such that
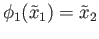 . Likewise
there exists a lift
. Likewise
there exists a lift
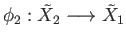 of the map
of the map 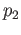 with respect to the covering
with respect to the covering
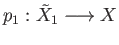 , such that
, such that
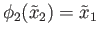 . From
. From
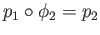 and
and
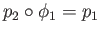 follows
follows
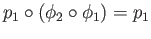 and
and
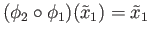 . Thus,
the identity map on
. Thus,
the identity map on
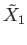 and
and
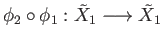 are both lifts of
are both lifts of
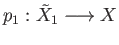 with respect to itself. By uniqueness of lifts we conclude that
with respect to itself. By uniqueness of lifts we conclude that
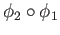 is the identity map on
is the identity map on
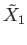 . Likewise
. Likewise
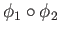 is the identity map on
is the identity map on
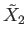 .
. 
nisha
2012-03-20