(i) Let 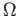 be a
simply connected open subset of
be a
simply connected open subset of
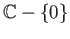 and
and
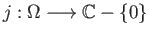 be the inclusion and
be the inclusion and
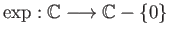 be the exponential map. Then
be the exponential map. Then  is a covering projection
with respect to which
is a covering projection
with respect to which 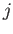 has a lift
has a lift
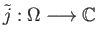 which means
which means
Thus there is a continuous branch of the logarithm on any simply connected open subset of
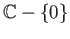 .
In the exercises the student is asked to show that any continuous lift is holomorphic.
.
In the exercises the student is asked to show that any continuous lift is holomorphic.
(ii) Consider the map
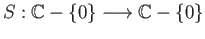 given by
given by
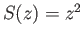 .
Let
.
Let
![$ \Omega = \mathbb{C} - [0, 1/2]$](img1522.png) and
and
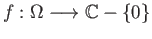 be given by
be given by
Let us determine the induced map
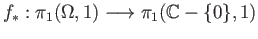 .
The group
.
The group
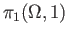 is the infinite cyclic group generated by the homotopy class of the loop
is the infinite cyclic group generated by the homotopy class of the loop
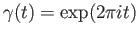 . Since
. Since
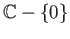 is a topological group under multiplication of complex numbers,
we may apply corollary (12.2) to get
is a topological group under multiplication of complex numbers,
we may apply corollary (12.2) to get
The additive notation is used for the infinite cyclic group.
The last equation may be rewritten as
since
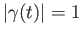 and the loop
and the loop
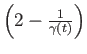 can be contracted to the constant loop in
can be contracted to the constant loop in
 . Hence
. Hence
The lifting criterion holds and  has a unique lift
has a unique lift
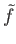 such that
such that
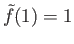 .
This lift is the continuous branch of
.
This lift is the continuous branch of
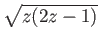 defined on
defined on 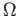 . In exercise 3,
the student is asked to show that the
lift
. In exercise 3,
the student is asked to show that the
lift
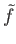 is holomorphic. Note that the space
is holomorphic. Note that the space 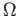 is not simply connected.
is not simply connected.
The next example is Picard's theorem which is a corollary of the following highly non-trivial
result.
nisha
2012-03-20
![]() given by
given by
![]() .
Let
.
Let
![]() and
and
![]() be given by
be given by
![$\displaystyle [f\circ\gamma(t)] = [\gamma(t)]+\Big[\gamma(t)\Big(2 - \frac{1}{\...
...ig)\Big]
= 2[\gamma(t)] + \Big[2 - \frac{1}{\gamma(t)}\Big] = 2, \eqno(18.6)
$](img1529.png)
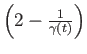 can be contracted to the constant loop in
can be contracted to the constant loop in