Let  and
and  be connected locally path connected spaces,
be connected locally path connected spaces,
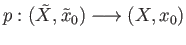 is a covering projection and
is a covering projection and
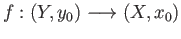 is a continuous function.
A lift
is a continuous function.
A lift
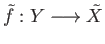 satisfying
satisfying
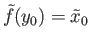 exists if and only if
exists if and only if
In particular, if  is simply connected, that is if
is simply connected, that is if
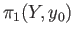 is trivial, then (18.1) holds
and the lift
is trivial, then (18.1) holds
and the lift
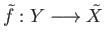 satisfying
satisfying
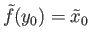 exists.
exists.
nisha
2012-03-20