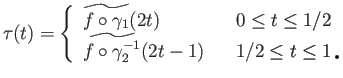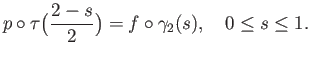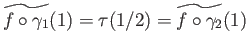To prove that the condition (18.1) is necessary, let us assume that a the lift exists.
Then
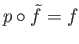 and
and
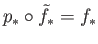 whereby,
whereby,
We now turn to the proof of sufficiency of (18.1). To construct the lift
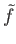 let
let 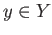 and
and  be a path in
be a path in  joining
joining 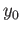 and
and 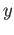 .
Take the lift of
.
Take the lift of
![$ f\circ \gamma : [0, 1]\longrightarrow X$](img1467.png) starting at
starting at
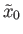 and we declare
and we declare
To show that the function
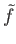 is well-defined, take two paths
is well-defined, take two paths 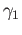 and
and 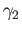 joining
joining 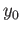 and
and 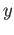 in
in  and form the closed loop
and form the closed loop
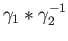 at
at 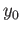 . Then
. Then
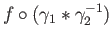 is a loop in
is a loop in  based at
based at  and
so
and
so
Choose a loop  in
in
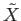 based at
based at
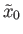 such that
such that
![$ p_*([\sigma]) = [f\circ (\gamma_1*\gamma^{-1}_2)]$](img1472.png) .
In other words, the loop
.
In other words, the loop
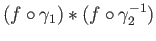 is homotopic to
is homotopic to
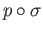 .
By the covering homotopy lemma,
The lift of
.
By the covering homotopy lemma,
The lift of
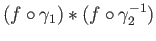 starting at
starting at
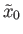 which will be denoted by
which will be denoted by 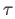 ,
is homotopic to
,
is homotopic to  . As a result,
. As a result, 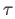 is also closed loop at
is also closed loop at
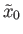 . Let
. Let
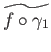 be the lift of
be the lift of
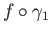 starting at
starting at
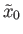 and
and
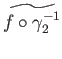 be the lift of
be the lift of
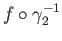 starting
at the terminal point
starting
at the terminal point
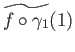 .
Observe that
.
Observe that
We now look at the projection of the two paths 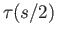 and
and
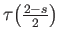 (
(
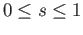 ):
):
and
The paths 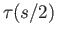 and
and
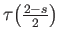 (
(
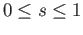 ) are thus lifts of
) are thus lifts of
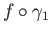 and
and
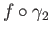 , both starting at
, both starting at
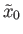 since
since 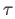 is a closed loop. Hence
is a closed loop. Hence
proving that
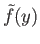 is well-defined.
nisha
2012-03-20
is well-defined.
nisha
2012-03-20
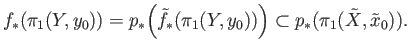
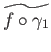 be the lift of
be the lift of
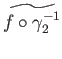 be the lift of
be the lift of
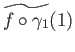 .
Observe that
.
Observe that