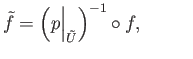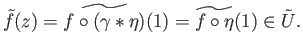Let 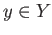 be arbitrary, and let
be arbitrary, and let 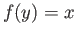 and
and
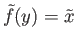 . Choose an evenly covered neighborhood
. Choose an evenly covered neighborhood  of
of 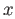 and
and
 be the sheet
containing
be the sheet
containing
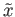 lying above
lying above  . By continuity of
. By continuity of  we obtain a neighborhood
we obtain a neighborhood  of
of 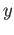 in
in  such that
such that
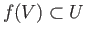 and hence
and hence
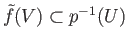 (since
(since
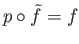 ).
).
Now if we assume that
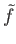 maps the neighborhood
maps the neighborhood  into
into
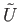 , then the following would be valid:
, then the following would be valid:
which would prove the continuity of
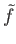 .
To prove that
.
To prove that
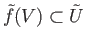 , we shall assume that the neighborhoods
, we shall assume that the neighborhoods  ,
,
 and
and
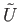 are path connected and invoke the construction of
are path connected and invoke the construction of
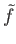 . Choose a path
. Choose a path
 in
in  joining
joining 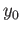 and
and 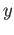 and for each
and for each  pick a path
pick a path 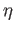 joining
joining 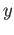 and
and 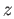 and then
we get the path
and then
we get the path
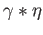 joining
joining 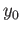 and
and 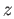 . Lift
. Lift
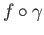 and
and
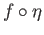 to paths in
to paths in 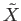 starting at
starting at
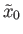 and
and
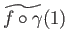 respectively. Since
respectively. Since
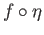 lies in
lies in  , its lift must lie entirely in
, its lift must lie entirely in 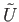 and hence
and hence
nisha
2012-03-20
![]() maps the neighborhood
maps the neighborhood ![]() into
into
![]() , then the following would be valid:
, then the following would be valid: