Rotor Action

At standstill, rotor conductors are being cut by rotating flux wave at synchronous speed n_s. Hence, the frequency f₂ of the rotor e.m.f and current is equal to the input voltage frequency f₁. When the rotor rotates at a speed of n_r rotations per second (r.p.s) in the direction of rotating flux wave, the relative speed between synchronously rotating flux and rotor conductors becomes ( n_s- n_r) r.p.s, i.e.,

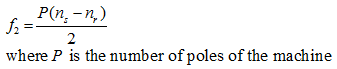(8)

Hence, the slip of the machine is defined as

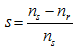(9)

Thus, the rotor frequency is defined as

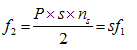(10)

At standstill the rotor frequency is f₁ and the field produced by rotor currents revolves at a speed equal to w.r.t. rotor structure. When the rotor rotates at a speed of nr, the rotor frequency is sf₁ and the rotor produced field revolves at a speed of w.r.t. rotor structure. The rotor is already rotating at a speed of n_r w.r.t. stator. Hence, the speed of rotor field w.r.t. to stator is equal to the sum of mechanical rotor speed nr and rotor field speed sn_s w.r.t. rotor. Hence, the speed of the rotor field with respect to stator is given by

(11)

The stator and rotor fields are stationary with respect to each other at all possible rotor speeds. Hence, a steady torque is produced by their interaction. The rotor of an induction motor can never attain synchronous speed. If does so then the rotor conductors will be stationary w.r.t. the synchronously rotating rotor conductors and hence, rotor m.m.f. would be zero.