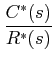 ,
,
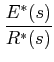 ,
,
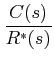 can be computed from Mason's gain formula, as:
can be computed from Mason's gain formula, as:
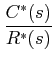 |
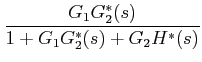 |
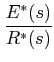 |
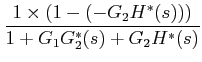 |
||
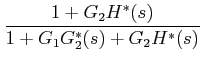 |
To derive
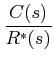 : Number of forward paths = 2 and the corresponding gains are
: Number of forward paths = 2 and the corresponding gains are
![% latex2html id marker 642
$\displaystyle \therefore \frac {C(s)}{R^{*}(s)}=\fr...
..._{2}H^{*}(s)]-G_{2}(s)H(s)G_{1}G_{2}^{*}(s)}{1+G_{1}G_{2}^{*}(s)+G_{2}H^{*}(s)}$](images/img42.png) |
Module 2 : Modeling Discrete Time Systems by Pulse Transfer Function
Lecture 5 : Sampled Signal Flow Graph
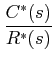 ,
,
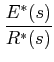 ,
,
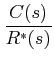 can be computed from Mason's gain formula, as:
can be computed from Mason's gain formula, as:
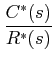 |
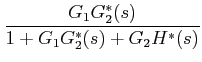 |
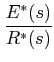 |
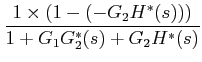 |
||
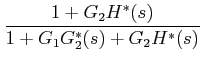 |
To derive
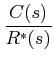 : Number of forward paths = 2 and the corresponding gains are
: Number of forward paths = 2 and the corresponding gains are
![% latex2html id marker 642
$\displaystyle \therefore \frac {C(s)}{R^{*}(s)}=\fr...
..._{2}H^{*}(s)]-G_{2}(s)H(s)G_{1}G_{2}^{*}(s)}{1+G_{1}G_{2}^{*}(s)+G_{2}H^{*}(s)}$](images/img42.png) |