| Solutions for temperature stress The Westergaard's (1926) equation for maximum tensile stress at the top for cental area of infinite slab due to negative temperature differential ( 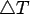 ) is: ) is:
The Westergaard expression for deflection and maximum tensile stress of semi infinite slab ( 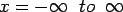 and and 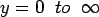 ) )
where, 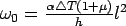 and and 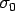 as expressed above. as expressed above.
The 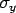 maximum occurs at maximum occurs at 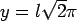 and the tensile stress at the edge location ( and the tensile stress at the edge location ( 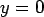 ), ), 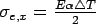 ; ; 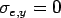 (Edge condition) (Edge condition)
For the slab with finite width ( 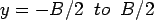 ) and infinite length ( ) and infinite length ( 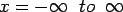 ), the deflection and stress equations are - ), the deflection and stress equations are -
where 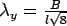 . Similar solution can be obtained for the slab with finite length ( . Similar solution can be obtained for the slab with finite length ( 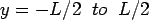 ) and infinite width ( ) and infinite width ( 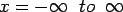 ) and taking, ) and taking, 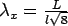 . .
The Bradbury (1938) equation for maximum tensile stress at the edge ( 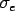 ) and interior ( ) and interior ( 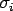 ) location with linear temperature gradient and finite slab with all edges free, over Winkler foundation are: ) location with linear temperature gradient and finite slab with all edges free, over Winkler foundation are:
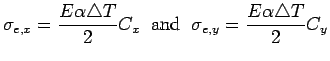 |
|
|
(22) |
![$\displaystyle \sigma_{i,x}=\frac{E \alpha \triangle T}{2(1-\mu^2)} \left[ C_x+ ... ...\sigma_{i,y}=\frac{E \alpha \triangle T}{2(1-\mu^2)}\left[ C_y+ \mu C_x \right]$](img162.png) |
|
|
(23) |
where,
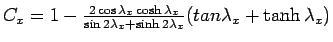 ; ; 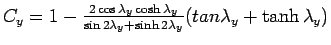 and, and, 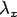 and and 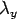 are same as above. are same as above.
The downward vertical displacement due to weight of slab
over a dense liquid foundation may be represented as:
The Westerdard solution is valid when 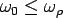 (slab in full contact). For large negative temperature differential ( (slab in full contact). For large negative temperature differential (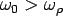 ) the slab may curled up and considering the gap due to curling, a closed form solution for semi-infinite slab can be presented as (Tang et al. 1993): ) the slab may curled up and considering the gap due to curling, a closed form solution for semi-infinite slab can be presented as (Tang et al. 1993):
where, 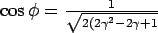 and and 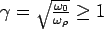 . .
The 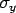 maximum occurs at maximum occurs at 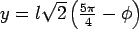 . When . When 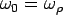 , then, , then, 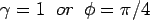 and thus it becomes the Westergaard's solution. For slab with finite width and infinite length, Westergaard's solution is valid when and thus it becomes the Westergaard's solution. For slab with finite width and infinite length, Westergaard's solution is valid when 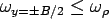 and and 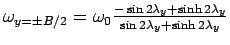 . The general solution proposed by Tang et al. (1993)is: . The general solution proposed by Tang et al. (1993)is:
|