Slab resting on Winkler foundation
In this type of foundation, the subgrade
is assumed to be composed of closely spaced linear
springs and subgrade shear strength is neglected.
The subgrade reaction is proportional to the deflection
(equivalent to dense liquid foundation) and the proportionality
(spring) constant is called as modulus of subgrade
reaction (k). So, the upward
subgrade pressure (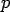 )
is )
is 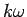 .
The equilibrium equation of plate resting on Winkler
foundation becomes: .
The equilibrium equation of plate resting on Winkler
foundation becomes:
where, radius of relative stiffness, 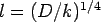 . .
The closed form solution for deflection due to slab wight (unit wight= 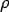 ) for finite dimensions ( ) for finite dimensions (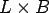 ) supported over an area in the middle by subgrade reaction may expressed as (Timoshenko, and Kreiger 1959): ) supported over an area in the middle by subgrade reaction may expressed as (Timoshenko, and Kreiger 1959):
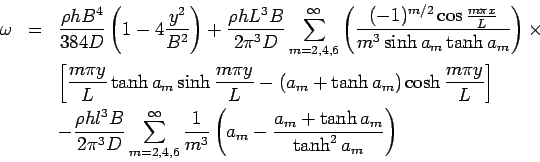
where, 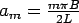 . .
Slab resting on Pasternak foundation
In this type of foundation, the shear interaction between the Winkler spring element is incorporated and subgrade shear force is assumed to be proportional to the variation in deflection in the soil layer (Cauwelaert et al. 2002). Therefore,
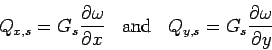
where, 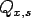 and and 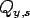 are the subgrade shear forces per unit length acting on the plane orthogonal to are the subgrade shear forces per unit length acting on the plane orthogonal to 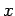 and and 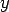 direction respectively and direction respectively and 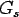 is called as subgrade shear modulus. So, the net upward vertical pressure ( is called as subgrade shear modulus. So, the net upward vertical pressure (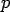 ) is: ) is:
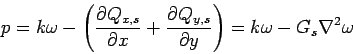
Therefore, the equilibrium equation for plate resting on Pasternak foundation become:
The Winkler foundation is a special case of Pasternak foundation (i.e when, 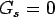 ). ).
Slab resting on Kerr foundation
In Kerr foundation, the subgrade is characterized with two spring constants ( 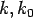 ) along with presence of subgrade shear interaction. The relationship between the upward subgrade reaction ( ) along with presence of subgrade shear interaction. The relationship between the upward subgrade reaction (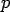 ) and deflection ( ) and deflection (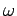 ) of the slab as follows (Cauwelaert et al. 2002): ) of the slab as follows (Cauwelaert et al. 2002):
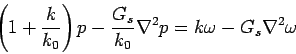
Therefore,
the equilibrium equation
(13) for Pasternak foundation becomes,
The Pasternak foundation is a special case of Kerr foundation (i.e when, 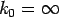 ). ).
|