Temperature stress analysis
Most of the studies show that the temperature distribution in concrete pavement is nonlinear.
Let, 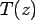 represent the pavement temperature at depth represent the pavement temperature at depth 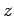 from the mid-surface (positive downward) and from the mid-surface (positive downward) and 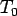 is the reference temperature at which the slab is free from any temperature stress. It is also assumed that elastic modulus ( is the reference temperature at which the slab is free from any temperature stress. It is also assumed that elastic modulus (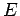 ) and Poisson's ratio ( ) and Poisson's ratio (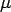 ) does not change with temperature and also the pavement temperature distribution of the pavement, with respect to time, is fixed. So, if the slab is fully restrained, the restrained strain ( ) does not change with temperature and also the pavement temperature distribution of the pavement, with respect to time, is fixed. So, if the slab is fully restrained, the restrained strain ( 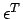 ) due to temperature change from ) due to temperature change from 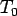 to to 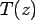 will be: will be:
|
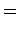 |
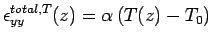 |
(17) |
The corresponding stress ( 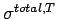 ), may be expressed as: ), may be expressed as:
where, 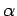 is coefficient
of thermal expansion of concrete. The positive strain indicates the compressive
stress (negative). It may be noted that the shape of the stress diagram is similar
to the temperature profile. The above stresses (equation 18 and 19) can be divided
into three components, (i) axial, (ii) bending and (iii) residual. This has been
explained schematically in Fig. 17 and Fig. 18, for day time and night time conditions
respectively (Choubane and Tia 1992). The various stress components are discussed
further in the following. is coefficient
of thermal expansion of concrete. The positive strain indicates the compressive
stress (negative). It may be noted that the shape of the stress diagram is similar
to the temperature profile. The above stresses (equation 18 and 19) can be divided
into three components, (i) axial, (ii) bending and (iii) residual. This has been
explained schematically in Fig. 17 and Fig. 18, for day time and night time conditions
respectively (Choubane and Tia 1992). The various stress components are discussed
further in the following.
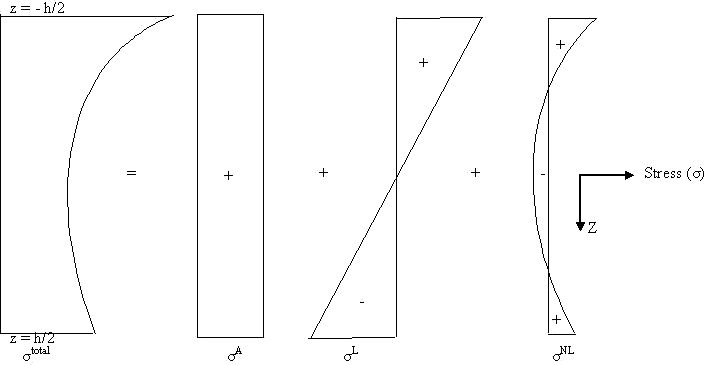 Figure
17. Various components of stress during day time
comdition Figure
17. Various components of stress during day time
comdition
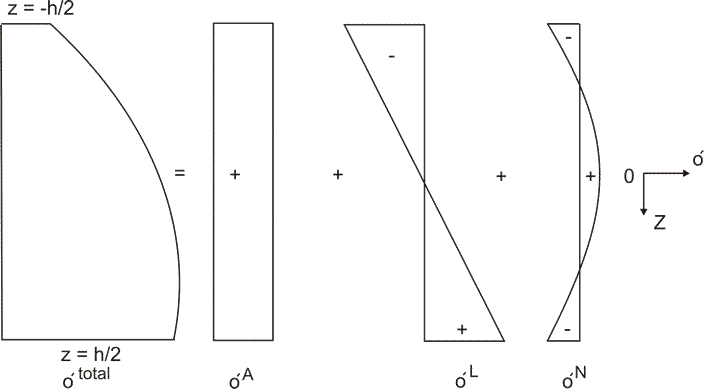
Figure
18: Various components of stress during night time condition
|