Axial stress component
It is assumed that the axial stress (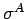 ), which is constant through the thickness of the slab, is generated due to axial temperature component, ), which is constant through the thickness of the slab, is generated due to axial temperature component, 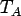 . The axial stress, . The axial stress, 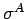 , can be obtained by equating thermal force due to , can be obtained by equating thermal force due to 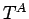 to the total thermal force produced by to the total thermal force produced by 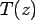 as shown in the following (Ioannides and Khazanovich 1998): as shown in the following (Ioannides and Khazanovich 1998):
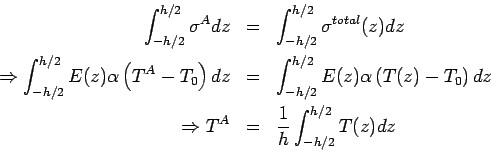
If 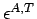 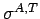 are axial strain and axial stress respectively, then are axial strain and axial stress respectively, then 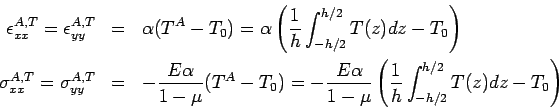
Most of the time concrete pavement is allowed to expand or contract through various joints. Thus, in such a situation, 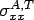 = = 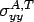 = = 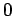 . .
Bending stress component
In a similar way, it is assumed that the bending stress (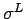 ), which varies linearly through the thickness of the slab and assumes a value of zero at the mid-plane of the cross-section, is generated due to bending (linear) temperature component, ), which varies linearly through the thickness of the slab and assumes a value of zero at the mid-plane of the cross-section, is generated due to bending (linear) temperature component, 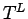 . The bending stress, . The bending stress,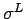 , can be obtained by equating thermal force due to , can be obtained by equating thermal force due to 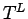 to the total thermal force produced by to the total thermal force produced by 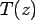 as shown in the following (Ioannides and Khazanovich 1998): as shown in the following (Ioannides and Khazanovich 1998):
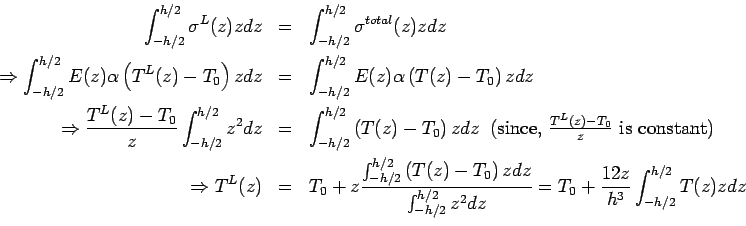
Accordingly, bending strain (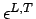 ) and bending stress ( ) and bending stress (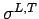 ) may be expressed as given below: ) may be expressed as given below:
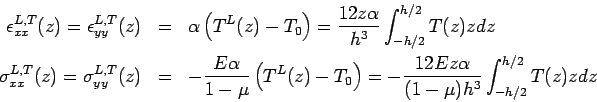
The maximum values of strain, stress and moment occur at the top (  ) and bottom ( ) and bottom (  ) and these values can be calculated as: ) and these values can be calculated as:
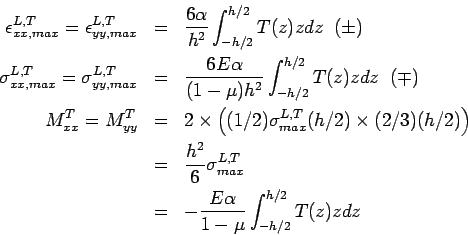
Most of the time the concrete pavement
is restrained against bending. This restraint is
primarily due to self weight of the slab. Thus, the
strain mentioned above is the restrained strain,
and the bending stress does develop in concrete pavement.
Residual stress component
The shape of 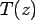 is arbitrary. Thus, combination of is arbitrary. Thus, combination of 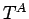 and and 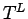 does not add up to does not add up to 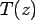 . Thus, . Thus, 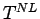 is the residual temperature component, obtained after deducting both the axial and linear temperature components from total temperature. The value of is the residual temperature component, obtained after deducting both the axial and linear temperature components from total temperature. The value of 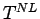 can be calculated as follows: can be calculated as follows:
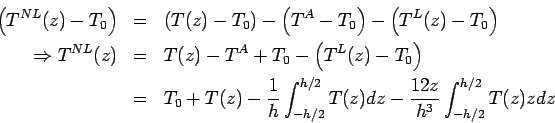
Thus, the restrained strain and the corresponding stress can be obtained as:
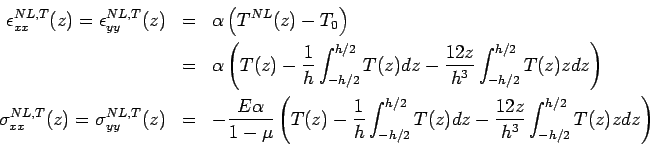
|