| Solutions for load stress The following are various solutions for load stress obtained by various researchers.
- Interior stress due to loading at interior (Westergaard 1926)
- Edge stress due to loading at edge (Westergaard 1926
- Corner stress due to loading at corner (Bradbury 1938, Fwa et al. 1996, Westergaard 1926)
Interior stress due to loading at interior (Westergaard 1926)
![\begin{eqnarray*} \sigma_{i,max} &=& \frac{3P(1+\mu)}{2 \pi h^2} \left[ \ln \lef... ...ight)+ \gamma - 1.25\right)\right]\;\;;\mbox{Westergaard (1926)} \end{eqnarray*}](img125.gif)
Edge stress due to loading at edge (Westergaard 1926)
![\begin{eqnarray*} \sigma_{e,max} &=& \frac{3P(1+\mu)}{\pi(3+\mu) h^2} \left[ \ln... ... \left( \frac{a}{l}\right) \right]\;\;;\mbox{Westergaard (1926)} \end{eqnarray*}](img126.gif)
Corner stress due to loading at corner (Bradbury 1938, Fwa et al. 1996, Westergaard 1926)
![\begin{eqnarray*} \sigma_{c,max} &=& \frac{3P}{h^2}\left[1-\left( \frac{1.4142a}... ...left[ 1- \frac{\sqrt 2 a}{l} \right] \;\;;\mbox{Spangler (1942)} \end{eqnarray*}](img127.gif)
where, radius of resisting section, ![$b=[1.6a^2+h^2]^{0.5} - 0.675h$](img128.png) ; if ; if 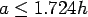 or or 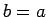 ; if ; if 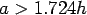 and Euler's constant, and Euler's constant, 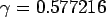 . .
|