Analysis of load stress
A concrete pavement is generally idealized as slab (or, plate) resting on elastic foundation. So as to develop the formulation for load stress calculation, the theory of plates is to be recapitulated first.
Basic theory of plates
For analysis purpose, a plate
can be assumed as infinite in both the directions,
semi-infinite, finite in one direction, or, finite
in both the directions and accordingly the reference
coordinates can be chosen. Figure
16 explains this configurations schematically.
For a basic plate analysis, it is assumed that the plate is homogenous, isotropic and elastic material and the cross section normal to the neutral axis remains plane before and after bending and, thus, there is no deformation along the thickness of plate. Therefore, the bending stress, 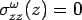 at any point across the depth ( at any point across the depth (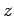 ) and the analysis becomes a plane stress case. For small deflection ( ) and the analysis becomes a plane stress case. For small deflection (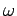 ) of plate (Timoshenko, and Kreiger 1959), it can be written, ) of plate (Timoshenko, and Kreiger 1959), it can be written, 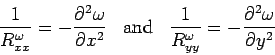
where, 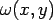 represents the deflection in Cartesian coordinate system along the z-direction (thickness) and represents the deflection in Cartesian coordinate system along the z-direction (thickness) and 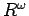 is the radius of curvature in the respective direction. The negative sign represents that the upward curvature is due to downward deflection. is the radius of curvature in the respective direction. The negative sign represents that the upward curvature is due to downward deflection.
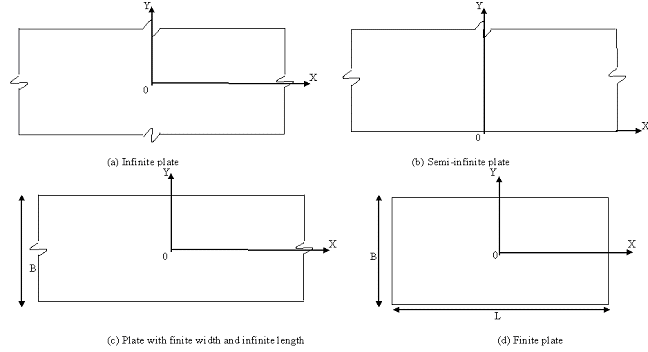
Figure 16: Various possible dimensions of a plate
Plate bending theory can be grossly grouped into two, thin plate theory and thick plate theory. For concrete pavement analysis purpose, it is generally assumed as thin plate. The assumption of thin plate (called as Kirchhoff plate) bending theory is that the thickness of the plate (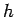 ) is small as compared to the other dimensions. Thus, the effects of ) is small as compared to the other dimensions. Thus, the effects of 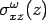 and and 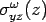 on bending are neglected where, on bending are neglected where, 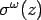 represent the bending stress due to external load in respective planes and represent the bending stress due to external load in respective planes and 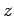 represent the depth from the neutral axis (Timoshenko, and Kreiger 1959). Thus, represent the depth from the neutral axis (Timoshenko, and Kreiger 1959). Thus,
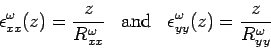
where, 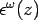 is the strain in the respective direction due to external load. So, the strain-deflection relationship due to bending may be presented as: is the strain in the respective direction due to external load. So, the strain-deflection relationship due to bending may be presented as:
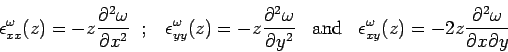
The strain-stress relationship due to bending may be represented as:
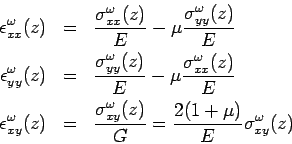
where, 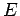 and and 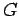 are the Young's modulus and shear modulus respectively (i.e. are the Young's modulus and shear modulus respectively (i.e. 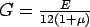 ). The bending stress-strain relationship due to external load becomes: ). The bending stress-strain relationship due to external load becomes:
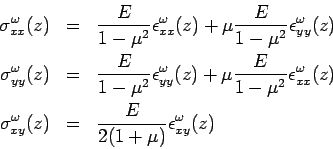
Therefore, the stress-deflection relationship may be expressed as:
If 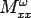 , , 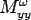 are the bending moments per unit length due to load, parallel to are the bending moments per unit length due to load, parallel to 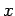 and and 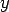 axis respectively, and axis respectively, and 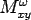 is the respective twisting moment in the is the respective twisting moment in the 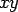 plane, then (Timoshenko, and Kreiger 1959), plane, then (Timoshenko, and Kreiger 1959),
where, flexural rigidity, 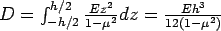 . Also, the stresses may be expressed as: . Also, the stresses may be expressed as:
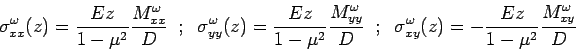
Let, 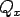 and and 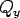 are the shear forces per unit length parallel to are the shear forces per unit length parallel to 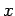 and and 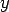 axis, then axis, then
If 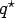 is the net pressure (downward positive) over the plate surface which may include the external load, subgrade reaction as well as self weight of the plate, then from the equilibrium considerations: is the net pressure (downward positive) over the plate surface which may include the external load, subgrade reaction as well as self weight of the plate, then from the equilibrium considerations:
|
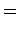 |
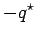 |
(12) |
Therefore, differentiating equation (10) with respect to 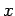 and
equation (11) with respect to and
equation (11) with respect to 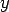 and,
then, substituting in equation (12), the equilibrium equation becomes (Timoshenko,
and Kreiger 1959): and,
then, substituting in equation (12), the equilibrium equation becomes (Timoshenko,
and Kreiger 1959):
where, 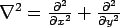 (Laplace biharmonic operator). (Laplace biharmonic operator).
When the
curvatures in x and y directions are equal such as
the case of symmetric interior loading, the deflection ( )
with free edges may be expressed as shown below: )
with free edges may be expressed as shown below:
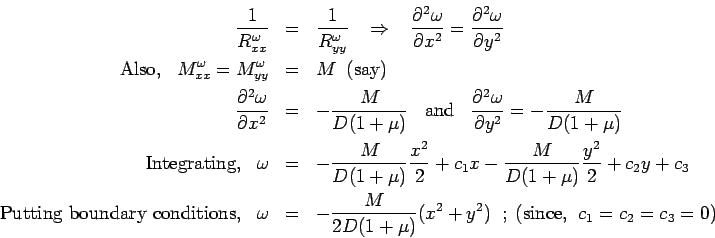 |