Module 3 : Microscopic Traffic Flow Modeling
Lecture 12 : Vehicle Arrival Models: Headway
1 2 3 4 5 6 7 8 9 10 11 12
 

Numerical Example

An observation from 2434 samples is given table below. Mean headway observed was 3.5 seconds and the standard deviation observed was 2.6 seconds. Fit a normal distribution, if we assume minimum expected headway is 0.5.
Table 1: Observed headway distribution
$ h$ $ h+dh$ $ p_i^o$
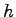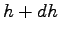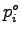0.0 1.0 0.012
1.0 2.0 0.178
2.0 3.0 0.316
3.0 4.0 0.218
4.0 5.0 0.108
5.0 6.0 0.055
6.0 7.0 0.033
7.0 8.0 0.022
8.0 9.0 0.013
9.0 $ >$ 0.045
Total   1.00

Solutions

The given headway range and the observed probability is given in column (2), (3) and (4). The observed frequency for the first interval (0 to 1) can be computed as the product of observed frequency $ p_i$ and the number of observation (N) i.e. $ p_i^o = p_i\times N = 0.012\times2434 = 29.21$ as shown in column (5). Compute the standard deviation to be used in calculation, given that $ \mu=3.5$, $ \sigma=2.6$, and $ \alpha=0.5$ as:
$\displaystyle \sigma$ $\displaystyle =$ $\displaystyle \frac{\mu-\alpha}{2}=\frac{3.5-0.5}{2}=1.5$  

Second, compute the probability that headway less than zero.
$\displaystyle p(t<0)$ $\displaystyle \approx$ $\displaystyle p\left(t\le \frac{0-3.5}{1.5}\right)$  
  $\displaystyle =$ $\displaystyle p(t\le -2.33) = 0.010$  

The value 0.01 is obtained for standard normal distribution table is shown in column (6). Similarly, compute the probability that headway less than 1.0 as:
$\displaystyle p(t\le 1)$ $\displaystyle \approx$ $\displaystyle p\left(t\le \frac{1.0-3.5}{1.5}\right)$  
  $\displaystyle =$ $\displaystyle p(t<-2)$  
  $\displaystyle =$ $\displaystyle 0.048$  

The value 0.048 is obtained from the standard normal distribution table is shown in column (6). Hence, the probability that headway between 0 and 1 is obtained using equation [*] as $ p(0\le t\le 1)$= $ 0.048-0.010 = 0.038$ and is shown in column (7). Now the computed frequency $ F_i^c$ is $ p(t<h<t+1)\times N = 0.038\times2434=92.431$ and is given in column (8). This procedure is repeated for all the subsequent items. It may be noted that probability of headway $ >$ 9.0 is computed by one minus probability of headway less than 9.0 $ =1-(0.038+0.111+\dots)=0.010.$
Table 2: Solution using normal distribution
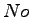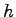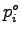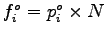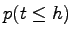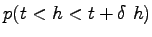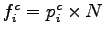$ No$ $ h$ $ h+\delta~h$ $ p_i^o$ $ f_i^o=p_i^o\times N$ $ p(t\leq h)$ $ p(t<h<t+\delta~h)$ $ f_i^c=p_i^c\times N$
(1) (2) (3) (4) (5) (6) (7) (8)
1 0.0 1.0 0.012 29.21 0.010 0.038 92.431
2 1.0 2.0 0.178 433.25 0.048 0.111 269.845
3 2.0 3.0 0.316 769.14 0.159 0.211 513.053
4 3.0 4.0 0.218 530.61 0.369 0.261 635.560
5 4.0 5.0 0.108 262.87 0.631 0.211 513.053
6 5.0 6.0 0.055 133.87 0.841 0.111 269.845
7 6.0 7.0 0.033 80.32 0.952 0.038 92.431
8 7.0 8.0 0.022 53.55 0.990 0.008 20.605
9 8.0 9.0 0.013 31.64 0.999 0.001 2.987
10 9.0 $ >$ 0.045 109.53 1.000 0.010 24.190
  Total   2434