| |
| | |
|
If one looks into traffic flow from a very long distance,
the flow of fairly heavy traffic appears like a stream of a
fluid.
Therefore, a macroscopic theory of traffic can be
developed with the help of hydrodynamic theory of fluids by
considering traffic as an effectively one-dimensional
compressible fluid.
The behaviour of individual vehicle is ignored and one is
concerned only with the behaviour of sizable aggregate of
vehicles.
The earliest traffic flow models began by writing the
balance equation to address vehicle number conservation on a
road.
In fact, all traffic flow models and theories must satisfy
the law of conservation of the number of vehicles on the
road.
Assuming that the vehicles are flowing from left to right,
the continuity equation can be written as
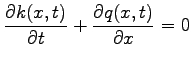 |
(1) |
where 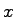 denotes the spatial coordinate in the direction of
traffic flow, denotes the spatial coordinate in the direction of
traffic flow, 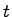 is the time, is the time, 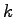 is the density and is the density and 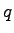 denotes the flow.
However, one cannot get two unknowns, namely
denotes the flow.
However, one cannot get two unknowns, namely 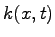 by and by and
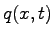 by solving one equation.
One possible solution is to write two equations from two
regimes of the flow, say before and after a bottleneck.
In this system the flow rate before and after will be same,
or by solving one equation.
One possible solution is to write two equations from two
regimes of the flow, say before and after a bottleneck.
In this system the flow rate before and after will be same,
or
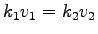 |
(2) |
From this the shock wave velocity can be derived as
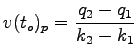 |
(3) |
This is normally referred to as Stock's shock wave formula.
An alternate possibility which Lighthill and Whitham adopted
in their landmark study is to assume that the flow rate 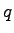 is determined primarily by the local density
is determined primarily by the local density 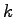 , so that
flow , so that
flow 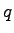 can be treated as a function of only density can be treated as a function of only density 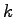 .
Therefore the number of unknown variables will be reduced to
one.
Essentially this assumption states that k(x,t) and q (x,t)
are not independent of each other.
Therefore the continuity equation takes the form .
Therefore the number of unknown variables will be reduced to
one.
Essentially this assumption states that k(x,t) and q (x,t)
are not independent of each other.
Therefore the continuity equation takes the form
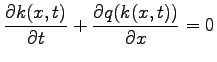 |
(4) |
However, the functional relationship between flow 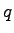 and
density and
density 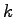 cannot be calculated from fluid-dynamical
theory.
This has to be either taken as a phenomenological relation
derived from the empirical observation or from microscopic
theories.
Therefore, the flow rate cannot be calculated from fluid-dynamical
theory.
This has to be either taken as a phenomenological relation
derived from the empirical observation or from microscopic
theories.
Therefore, the flow rate 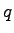 is a function of the vehicular
density k; is a function of the vehicular
density k; 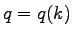 .
Thus, the balance equation takes the form .
Thus, the balance equation takes the form
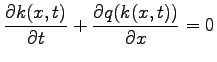 |
(5) |
Now there is only one independent variable in the balance
equation, the vehicle density 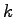 .
If initial and boundary conditions are known, this can be
solved.
Solution to LWR models are kinematic waves moving with
velocity .
If initial and boundary conditions are known, this can be
solved.
Solution to LWR models are kinematic waves moving with
velocity
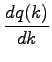 |
(6) |
This velocity 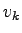 is positive when the flow rate increases
with density, and it is negative when the flow rate
decreases with density.
In some cases, this function may shift from one regime to
the other, and then a shock is said to be formed.
This shock wave propagate at the velocity is positive when the flow rate increases
with density, and it is negative when the flow rate
decreases with density.
In some cases, this function may shift from one regime to
the other, and then a shock is said to be formed.
This shock wave propagate at the velocity
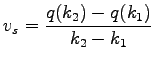 |
(7) |
where 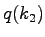 and and 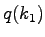 are the flow rates corresponding
to the upstream density are the flow rates corresponding
to the upstream density 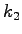 and downstream density and downstream density 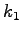 of the shock wave.
Unlike Stock's shock wave formula there is only one variable
here.
of the shock wave.
Unlike Stock's shock wave formula there is only one variable
here.
|
|
| | |
|
|
|