| |
| | |
|
Macroscopic stream models represent how the behaviour of one parameter of
traffic flow changes with respect to another.
Most important among them is the relation between speed and density.
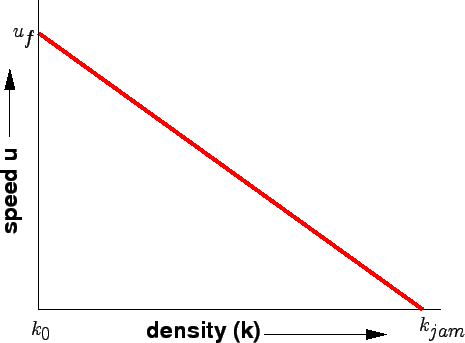
The first and most simple relation between them is proposed by Greenshield.
Greenshield assumed a linear speed-density relationship as illustrated in
figure 1 to derive the model.
Figure 1:
Relation between speed and density
 |
The equation for this relationship is shown below.
![$\displaystyle v = v_f -\left[\frac{v_f}{k_j}\right].k$](img2.png) |
(1) |
where 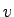 is the mean speed at density is the mean speed at density 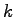 , , 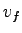 is the free speed and is the free speed and 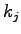 is
the jam density.
This equation ( 1) is often referred to as the Greenshield's model.
It indicates that when density becomes zero, speed approaches free flow speed
(ie. is
the jam density.
This equation ( 1) is often referred to as the Greenshield's model.
It indicates that when density becomes zero, speed approaches free flow speed
(ie.
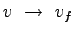 when when
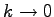 ). ).
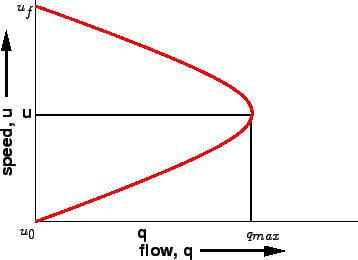
Figure 2:
Relation between speed and flow
 |
Once the relation between speed and flow is established, the relation with flow
can be derived.
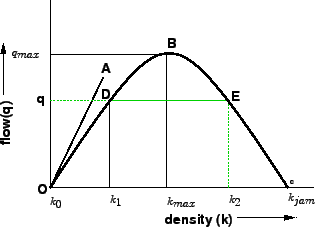
This relation between flow and density is parabolic in shape and is shown in
figure 3.
Also, we know that
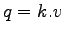 |
(2) |
Figure 3:
Relation between flow and density 1
 |
Now substituting equation 1 in equation 2, we get
![$\displaystyle q = v_f.k -\left [{\frac{v_f}{k_j}}\right] k^2$](img12.png) |
(3) |
Similarly we can find the relation between speed and flow.
For this, put
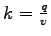 in equation 1 and solving, we get in equation 1 and solving, we get
![$\displaystyle q = k_j.v -\left[{\frac{k_j}{v_f}}\right] v^2$](img14.png) |
(4) |
This relationship is again parabolic and is shown in figure 2.
Once the relationship between the fundamental variables of traffic flow is
established, the boundary conditions can be derived.
The boundary conditions that are of interest are jam density, free-flow speed,
and maximum flow.
To find density at maximum flow, differentiate equation 3 with
respect to 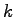 and equate it to zero. ie., and equate it to zero. ie.,
Denoting the density corresponding to maximum flow as 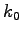 , ,
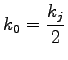 |
(5) |
Therefore, density corresponding to maximum flow is half the jam density.
Once we get 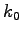 , we can derive for maximum flow, , we can derive for maximum flow, 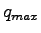 .
Substituting equation 5 in equation 3 .
Substituting equation 5 in equation 3
Thus the maximum flow is one fourth the product of free flow and jam density.
Finally to get the speed at maximum flow, 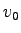 , substitute
equation 5 in equation 1 and solving we get, , substitute
equation 5 in equation 1 and solving we get,
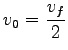 |
(6) |
Therefore, speed at maximum flow is half of the free speed.
|
|
| | |
|
|
|