Module 1 : Traffic Stream Characteristics

Lecture 03 : Traffic Stream Models

1

2

3

4

5

6

7

8

9

	Other macroscopic stream models In Greenshield's model, linear relationship between speed and density was assumed. But in field we can hardly find such a relationship between speed and density. Therefore, the validity of Greenshield's model was questioned and many other models came up. Prominent among them are Greenberg's logarithmic model, Underwood's exponential model, Pipe's generalized model, and multi-regime models. These are briefly discussed below. 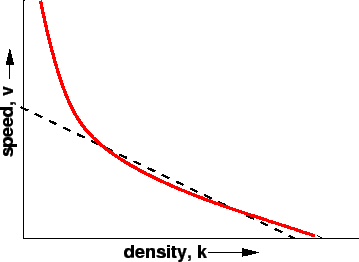Greenberg's logarithmic model Greenberg assumed a logarithmic relation between speed and density. He proposed, Figure 1: Greenberg's logarithmic model 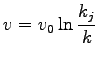$$v = v_0 \ln \frac{k_j}{k}$$ (1) This model has gained very good popularity because this model can be derived analytically. (This derivation is beyond the scope of this notes). However, main drawbacks of this model is that as density tends to zero, speed tends to infinity. This shows the inability of the model to predict the speeds at lower densities.