 |
Field due to an infinite charged sheet with surface charge density 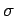 |
| |
Choose a cylindrical Gaussian pillbox of height 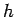 (with (with 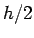 above the sheet and above the sheet and 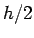 below the sheet) and radius below the sheet) and radius 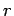 . .
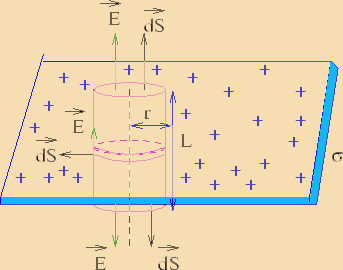 Click here for Animation Click here for Animation
The amount of charge enclosed is area times the surface charge density, i.e., 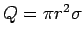 . By symmetry, the field is directed perpendicular to the sheet, upward at points above the sheet and downward for points below. There is no contribution to the flux from the curved surface. The flux from the two end faces is . By symmetry, the field is directed perpendicular to the sheet, upward at points above the sheet and downward for points below. There is no contribution to the flux from the curved surface. The flux from the two end faces is 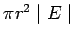 each, each,
|