 |
Applications of Gauss's Law |
| |
Field due to a uniformly charged sphere of radius with a charge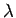 |
| |
Gaussian surface is a cylinder of radius 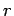 and length and length 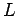 . . |
| |
By symmetry, the field is radial. Gaussian surface is a concentric sphere of radius 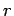 . The outward normals to the Gaussian surface is parallel to the field at every point. Hence For , . The outward normals to the Gaussian surface is parallel to the field at every point. Hence For , |
| |
|
| |
so that |
| |
|
| |
The field outside the sphere is what it would be if all the charge is concentrated at the origin of the sphere.
For , a fraction of the total charge is enclosed within the gaussian surface, so that |
| |
|
| |
The field inside is |
| |
Exercise |
| |
|