| |
We define the flux of the electric field through an area 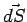 to be given by the scalar product to be given by the scalar product |
| |
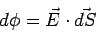 If If 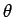 is the angle between the electric field and the area vector is the angle between the electric field and the area vector 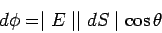 |
| |
For an arbitrary surface S, the flux is obtainted by integrating over all the surface elements |
| |
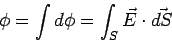 |
| |
If the electric field is uniform, the angle 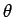 is constant and we have is constant and we have |
| |
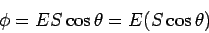 |
| |
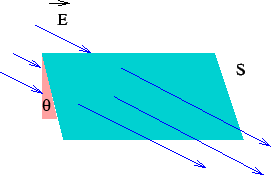
Thus the flux is equal to the product of magnitude of the electric field and the projection of area perpendicular to the field. |
| |
 |
| |
|
| |
Unit of flux is N-m 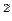 /C. Flux is positive if the field lines come out of the surface and is negative if they go into it. /C. Flux is positive if the field lines come out of the surface and is negative if they go into it. |
| |
|