 |
i.e. a total outward flux of 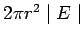 . Hence . Hence |
| |
where 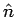 is a unit vector perpendicular to the sheet, directed upward for points above and downwards for points below (opposite, if the charge density is negative). is a unit vector perpendicular to the sheet, directed upward for points above and downwards for points below (opposite, if the charge density is negative). |
| |
Field due to a uniformly charged sphere of radius 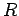 with a charge with a charge 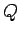 |
| |
By symmetry, the field is radial. Gaussian surface is a concentric sphere of radius 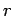 . The outward normals to the Gaussian surface is parallel to the field . The outward normals to the Gaussian surface is parallel to the field 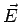 at every point. Hence at every point. Hence 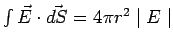 |