| |
Solid Angle : |
 |
The concept of solid angle is a natural extension of a plane angle to three dimensions. Consider an area element dS at a distance 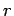 from a point P. Let be the unit vector along the outward normal to . |
| |
The element of the solid angle subtended by the area element at P is defined as |
| |
|
| |
where is the projection of along a direction perpendicular to . If is the angle betwe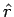en  and , then, |
| |
|
| |
|
| |
Solid angle is dimensionless. However, for practical reasons it is measured in terms of a unit called steradian (much like the way a planar angle is measured in terms of degrees). |
| |
The maximum possible value of solid angle is , which is the angle subtended by an area which encloses the point P completely. |
| |
Example |
| |
Exercise |
| |
Example 3 |
| |
Example 4 |
| |
Example 5 |
| |
Example 6 |
