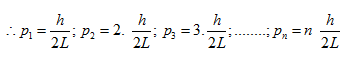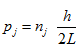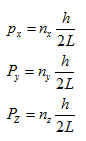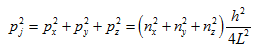** A stationary wave is equivalent to two traveling waves propagating in opposite directions, the waves being reflected and re-reflected at the ends of the string. This is analogous to the motion of a particle moving freely back and forth along a straight line and making elastic collisions at two points separated by the distance L.

According to quantum mechanics, a stationary Schrodinger wave is in fact completely equivalent to such a particle, and the wavelength λ of the stationary wave is related to the momentum p of the particle through the relation

(5.21)

where h = Planck's constant. The momentum of the particle for different nodes/antinodes are

(5.22)

It can be observed that the momentum of the particle is not continuous rather it is discrete. We can write down the momentum of a particle in the form

(5.23)

If the particle is free to move in any direction within a cubical box of side length L whose sides are parallel to the x, y and z axes of a rectangular co-ordinate system, the x, y and z components of its momentum are permitted to have only the values

(5.24)

where n_x, n_y and n_z are integers called the quantum numbers, each of which can have some one of the values 1, 2, 3, etc.

Each set of quantum numbers corresponds to a certain direction of momentum.

If p_j is the resultant momentum corresponding to some set of quantum numbers n_x, n_y & n_z,

(5.25)

If we let

(5.26)