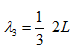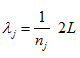Energy States and Energy Levels

As discussed in the previous section, classical mechanics does not apply at microscopic scale. For such analysis, quantum mechanics (wave mechanics) is applied.

In quantum theory, to each energy level there correspond one or more quantum states described by a wave function Ψ. For so-called stationary states, Ψ will be a function dependent on the position coordinates and time. When there are several quantum states that have the same energy, the states are said to be degenerate . The quantum state associated with the lowest energy level is called the ground state of the system ; those that correspond to higher energies are called excited states . The energy levels can be thought of as a set of shelves at different heights, while quantum states correspond to a set of boxes on each shelf. For each energy level ε_i the number of quantum states is given by the degeneracy g_i .

General method of attacking a problem of quantum mechanics/wave mechanics is to set up and solve an equation known as Schrodinger's equation. In many problems, this equation is exactly analogous to the wave equation describing the propagation of transverse in a stretched string, fixed at both ends. As is well known, the string can vibrate in a steady state in any one of a number of stationary waves (Fig. 5.1).

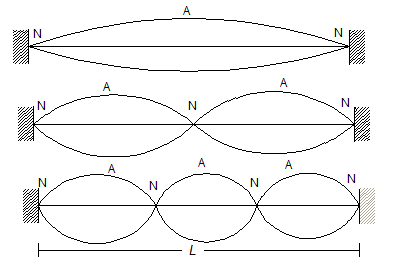
Fig. 5.1 Stationary waves in a stretched string fixed at both end

There may be a node N at each end and an anti node A at the center, or there may be a node at the center as well as at the ends, with anti nodes midway between the nodes, and so on. There is always an integral number of antinodes in the steady state modes of vibration. Distance between nodes (or anti nodes) is one half of the wave length, so if L is the length of the string, the wave length λ of the possible stationary waves** are

λ1 = 2L

(5.17)

λ2 = ½ 2L

(5.18)

(5.19)

(5.20)

where n_j is an integer equal to the number of anti nodes and can have some one of the values

n_j = 1, 2, 3..........