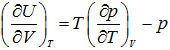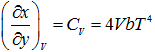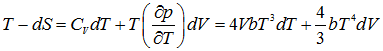Application of energy equation for thermal radiation in equilibrium with the enclosure walls
Let, u = energy density

p = radiation pressure exerted by a black body in an enclosure ( from electro magnetic theory) =

Blackbody raditation is thus specified by the pressure, volume and temperature of radiation.

U = uV

1.174

1.175

1.176

1.177

Energy Equation is

1.178

Substituting in energy equation

1.179

1.180

On integration,

u = bT4

1.181

where b is a constant.

Eq.(1.181) is known as Stefan-Boltzmann equation.

Since,

U = uV = VbT4

1.182

1.183

And,

1.184

From first T - dS relation,

1.185

For a reversible isothermal change of volume, the heat is to be supplied reversibly to keep temperature constant [TdS = Q].

1.186

For a reversible adiabatic change of volume,

1.187

[Q = 0]

or,

1.188

or,

VT3 = Constant

1.189

If the temperature is one half of the original temperature, the volume of the blackbody radiation is to be increased adiabatically 8 times its original volume so that the radiation remains in equilibrium with the matter at that temperature.