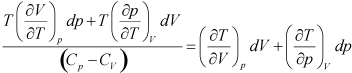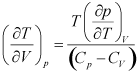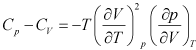From the first and second T - dS relations we can write,

1.136

or,

1.137

or,

1.138

Again,

1.139

or,

1.140

Equating the coefficient of dV

1.141

1.142

Similarly,

1.143

From Theorem 3,

1.144

Hence,

1.145

Following interpretations can be made from Eq. (1.145)

Since 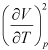is always positive and 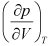for any substance is always negative, the difference of specific heats (C_P - C_V) is always positive.
As T → 0, C_P → C_V. In other words, C_P = C_V at absolute zero temperature.
When 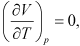then C_P = C_V
For an ideal gas, pV = mRT

Hence, C_P - C_V = mR

or, C_P - C_V = R